Räta linjens ekvation från grunden

Räta linjens ekvation, som oftast dyker upp i formen y = kx + m, är ett av matematikens mest kraftfulla grundverktyg. Den låter oss beskriva och förutse samband där förändringen sker i en jämn, förutsägbar takt – något vi stöter på överallt i vardagen.

Vad betyder egentligen y = kx + m?

Att greppa räta linjens ekvation är enklare än man tror. Föreställ dig att du ska ut på en roadtrip. Ekvationen y = kx + m fungerar då som en slags karta över din resa, där varje del har en specifik betydelse.

Allt börjar med m-värdet. Det här är din startpunkt, alltså var du befinner dig innan du ens vridit om nyckeln. I ett koordinatsystem är det helt enkelt den punkt där linjen skär den lodräta y-axeln.

Sedan har vi k-värdet, som också kallas för lutning eller riktningskoefficient. Det här representerar din hastighet – hur snabbt avståndet (y) förändras för varje timme (x) du kör. I grund och botten beskriver k-värdet hur brant och åt vilket håll din linje lutar.

Förstå k-värdets roll

Det är k-värdet som verkligen ger linjen sin unika karaktär. Det talar om exakt hur mycket y-värdet förändras för varje enstaka steg vi tar åt höger längs x-axeln. Man kan se det på tre olika sätt:

• Positiv lutning (k > 0): Linjen pekar uppåt, från vänster till höger. När x ökar, så ökar även y. Tänk dig att du kör uppför en backe.
• Negativ lutning (k < 0): Linjen pekar istället nedåt. För varje steg du tar i x-led, minskar y-värdet. Det här är som att köra i en nedförsbacke.
• Noll-lutning (k = 0): Linjen är helt platt, en horisontell linje. Y-värdet är konstant och ändras aldrig, oavsett hur stort x blir. Perfekt raksträcka!

Räta linjens ekvation är en så grundläggande modell för att beskriva linjära samband att den är en av de första sakerna man lär sig i svensk skola.

Den är en absolut hörnsten i gymnasiets första matematikkurs. Faktum är att statistik visar att runt 75 % av eleverna i årskurs 2 på gymnasiet klarar kunskapsmålen för linjära funktioner, vilket säger en del om hur central den här kunskapen anses vara. Om du vill fördjupa dig kan du läsa mer om räta linjens ekvation i gymnasiekursen på Matteboken.se.

När du väl förstår hur de här två delarna, m och k, spelar ihop kan du inte bara rita upp en linje, utan också tolka och förutse vad som händer i verkliga situationer.

Så räknar du fram ekvationen, steg för steg

Okej, nu är det dags att gå från teori till praktik. Att förstå vad k och m betyder är en sak, men att själv kunna räkna fram en räta linjens ekvation är det som verkligen gör skillnad. Det är nyckeln till att knäcka den här typen av uppgifter.

Vi ska kika på de två vanligaste situationerna du kommer att stöta på, både i skolan och på högskoleprovet. Det första är när du har två punkter som linjen går igenom. Det andra är när du får en punkt och ett k-värde serverat. Båda metoderna är raka och lätta att följa när man väl kan stegen.

Tänk på det så här: m-värdet är din startpunkt och k-värdet är din hastighet. Tillsammans bestämmer de exakt var du hamnar (ditt y-värde) vid en viss tidpunkt (ditt x-värde).

Bilden ovan fångar den tanken ganska bra. Du har ett utgångsläge (m) och en motor för förändring (k), vilket ger ett specifikt resultat (y) för varje givet x.

Hitta ekvationen med hjälp av två punkter

Låt oss ta ett konkret exempel. Tänk dig att en linje passerar genom punkterna (2, 9) och (4, 15). Vårt uppdrag är att hitta den y = kx + m-ekvation som beskriver just den linjen.

1. Räkna ut k-värdet (lutningen)

Det första vi måste göra är att ta reda på hur mycket linjen lutar. Det gör vi med den klassiska formeln som mäter förändringen i höjdled delat med förändringen i sidled.

Formeln är: k = (y₂ - y₁) / (x₂ - x₁)

• Vi matar in våra värden: k = (15 - 9) / (4 - 2)
• Sedan räknar vi: k = 6 / 2
• Och får resultatet: k = 3

Perfekt, nu vet vi att linjens lutning är 3. Skulle du stöta på en uträkning som ger ett bråktal kan du fräscha upp minnet med vår guide om att räkna med bråktal.

2. Lös ut m-värdet (där linjen korsar y-axeln)

Eftersom vi nu vet att k = 3, ser vår ekvation ut så här: y = 3x + m. För att hitta m behöver vi bara låna koordinaterna från en av våra punkter – vilken som helst funkar. Vi tar den första, (2, 9).

• Sätt in x=2 och y=9 i ekvationen: 9 = 3 * 2 + m
• Förenkla högersidan: 9 = 6 + m
• Lös ut m: m = 9 - 6
• Resultatet blir: m = 3

Klart! Ekvationen för linjen som går igenom punkterna (2, 9) och (4, 15) är alltså y = 3x + 3.

Hitta ekvationen med en punkt och ett k-värde

Det andra vanliga scenariot är faktiskt ännu enklare. Föreställ dig att du redan vet att en linje har lutningen k = -2 och att den passerar genom punkten (3, 4).

1. Utgå från det du vet

Vi har ju redan k-värdet, så vi kan direkt skriva ner en nästan färdig ekvation: y = -2x + m. Den enda pusselbiten som saknas är m.

2. Använd punkten för att hitta m

Precis som i förra exemplet använder vi punktens koordinater (x=3 och y=4) och sätter in dem i vår halvfärdiga ekvation.

• Sätt in värdena: 4 = -2 * 3 + m
• Förenkla: 4 = -6 + m
• Lös ut m: m = 4 + 6
• Resultat: m = 10

Då är vi hemma! Ekvationen för den här linjen är y = -2x + 10. Med de här två metoderna i verktygslådan har du en stabil grund för att lösa de flesta uppgifter som rör räta linjens ekvation.

Linjens ekvation – mer än bara y = kx + m

De flesta av oss tänker nog direkt på y = kx + m när vi hör "räta linjens ekvation". Det är ju den formen vi lär oss i skolan, och den är fantastisk på många sätt. Men den är bara en av flera verktyg i den matematiska verktygslådan. Att känna till de andra formerna ger dig fler vägar att lösa ett problem, vilket är guld värt när klockan tickar under högskoleprovet.

Man kan se de olika formerna som olika språk. Ibland är det enklast att beskriva något på ett visst sätt, beroende på vilken information du har från början. Att kunna "prata" alla tre flytande gör dig till en mycket mer flexibel och effektiv problemlösare.

K-formen: y = kx + m

Det här är den klassiska och mest visuella formen. Styrkan ligger i hur otroligt tydligt den visar linjens två absolut viktigaste egenskaper: lutningen (k) och punkten där den korsar y-axeln (m).

Ska du snabbt skissa en graf eller förstå hur en linje beter sig? Då är k-formen din bästa vän. Den ger dig direkta svar på frågorna "Hur brant lutar den?" och "Var på y-axeln börjar den?". Enkelt och rakt på sak.

Den har dock en liten akilleshäl – den klarar inte av att beskriva helt lodräta linjer. Eftersom en vertikal linje har en odefinierbar, "oändlig" lutning, kan man inte sätta in något värde för k. Då får man ta till andra metoder.

Enpunktsformeln: y - y₁ = k(x - x₁)

Enpunktsformeln är en riktig pärla när du har en specifik typ av information. Den är skräddarsydd för det vanliga scenariot där du känner till linjens lutning (k) och en enda punkt (x₁, y₁) som linjen passerar.

Istället för att först krångla med att räkna ut m-värdet (som du måste i k-formen), stoppar du bara in de värden du har direkt i formeln. Klart!

Tänk på enpunktsformeln som en smart genväg. Den tar informationen du har – en punkt och en lutning – och bygger ekvationen åt dig direkt, utan några extra steg.

Det här sparar inte bara dyrbar tid, utan minskar också risken för onödiga slarvfel. Formeln är extra vass i uppgifter som rör parallella eller vinkelräta linjer, där du ofta får just en lutning och en punkt. Att ha koll på den här är en av de där smarta matematik-strategier för högskoleprovet som verkligen kan göra skillnad.

Allmän form: Ax + By + C = 0

Vid första anblicken kan den allmänna formen kännas lite klumpig och mindre intuitiv. Alla termer är samlade på ena sidan, och A, B och C är oftast heltal. Men den har en superstyrka som de andra saknar: den kan beskriva precis alla räta linjer. Inga undantag.

Den klarar till och med av de vertikala linjerna som k-formen misslyckades med. En linje som x = 5 kan till exempel skrivas som 1x + 0y - 5 = 0. Det gör den allmänna formen väldigt robust och den används flitigt i mer avancerad matematik och programmering.

Att kunna skriva om en ekvation från k-form till allmän form (och tvärtom) är en nyckelkompetens. Det visar att du verkligen har grepp om hur linjära samband fungerar på djupet.

Jämförelse av räta linjens ekvationsformer

För att ge en tydlig överblick över de tre vanligaste formerna för räta linjens ekvation, deras struktur och när de passar bäst, har vi sammanställt en tabell.

Form	Struktur	Bästa användningsområde	Exempel (Linjen y = 2x + 3)
K-form	y = kx + m	När lutning (k) och y-intercept (m) är kända eller ska visas tydligt. Perfekt för att snabbt rita en graf.	y = 2x + 3
Enpunktsform	y - y₁ = k(x - x₁)	När en punkt (x₁, y₁) och lutningen (k) är givna. Snabbast för att bygga en ekvation från denna information.	y - 5 = 2(x - 1) (med punkten 1,5)
Allmän form	Ax + By + C = 0	När alla linjer, inklusive vertikala, måste kunna representeras. Används ofta i mer avancerad matematik.	2x - y + 3 = 0

Genom att förstå styrkorna hos varje form kan du välja det mest effektiva verktyget för varje unikt problem du ställs inför.

Från ekvation till graf på två enkla sätt

Att kunna ta en abstrakt formel som räta linjens ekvation och förvandla den till en bild är en av de där grundläggande superkrafterna i matten. Plötsligt kan du se sambandet framför dig. Som tur är finns det två riktigt bra och pålitliga metoder för att rita grafen.

Den ena är snabb och lite elegant, perfekt för snabba skisser. Den andra är mer metodisk och nästan idiotsäker. Båda ger dig exakt samma resultat: en perfekt ritad linje i ett koordinatsystem. Vi kikar på båda, steg för steg.

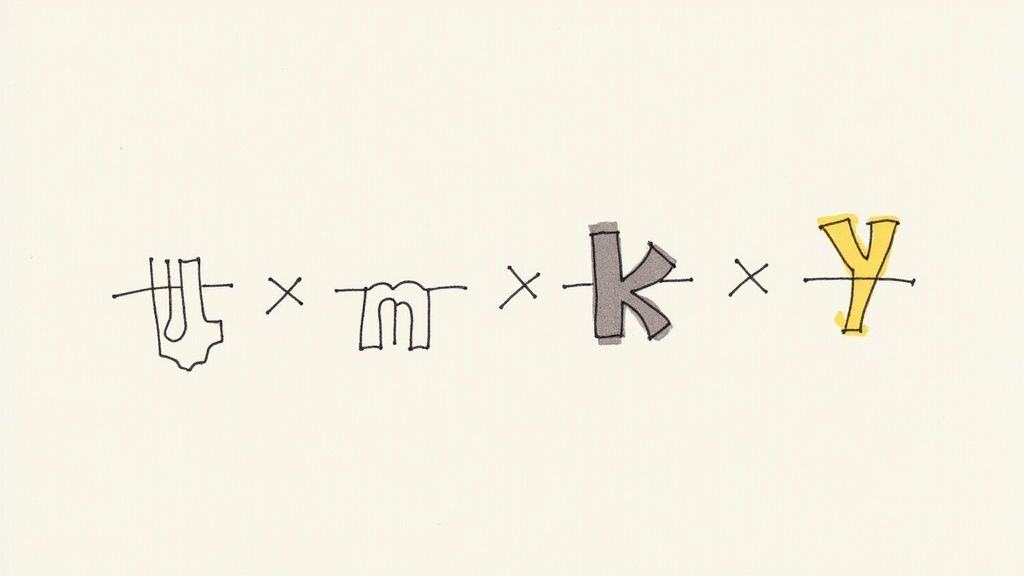
Metod 1: Starta med m och följ k-värdet

Den här metoden, som ibland kallas för m- och k-metoden, är överlägset snabbast när du har en ekvation på den klassiska k-formen, y = kx + m. Hela idén är att se ekvationens delar som direkta instruktioner för hur du ska rita.

Tänk dig att vi har ekvationen y = 2x + 1. Så här gör du:

1. Hitta din startpunkt. Kolla på m-värdet, som här är +1. Det är din utgångspunkt – punkten där linjen skär y-axeln. Sätt en prick på koordinaten (0, 1).
2. Använd k-värdet som vägbeskrivning. k-värdet är 2. Tänk på det som bråket 2/1. Det här kan du översätta till en enkel regel: "för varje steg du går åt höger (nämnaren 1), ska du gå två steg uppåt (täljaren 2)".
3. Hitta nästa punkt. Från din startpunkt (0, 1), ta ett steg åt höger och två steg upp. Där har du din andra punkt: (1, 3). Markera den också.
4. Dra linjen. Två punkter är allt som behövs. Ta en linjal, dra ett streck genom (0, 1) och (1, 3), och du är klar!

Metoden är otroligt smidig för att snabbt få en känsla för hur en linje ser ut, var den ligger och hur brant den är.

Metod 2: Bygg en värdetabell

Värdetabellen är den mer grundliga och systematiska metoden som funkar i alla lägen, oavsett hur krånglig ekvationen ser ut. Det handlar helt enkelt om att välja ut några x-värden, stoppa in dem i formeln och se vilka y-värden som kommer ut.

Vi kör med samma ekvation igen: y = 2x + 1.

Börja med att rita upp en enkel tabell. Välj sedan några x-värden som är lätta att räkna med. Noll är nästan alltid ett måste, och sen ett positivt och ett negativt tal för att få bra spridning.

x	y = 2x + 1	y	Punkt
-1	y = 2(-1) + 1 = -2 + 1	-1	(-1, -1)
0	y = 2(0) + 1 = 0 + 1	1	(0, 1)
2	y = 2(2) + 1 = 4 + 1	5	(2, 5)

Ett litet proffstips är att alltid välja x = 0. Det ger dig direkt linjens m-värde på silverfat. I vårt exempel ser vi ju att när x är 0 så blir y lika med 1 – precis som m-värdet i formeln.

När du har räknat fram dina punkter är det bara att pricka in dem i koordinatsystemet och dra en linje genom dem. Den stora fördelen här är säkerheten. Om dina tre punkter mot förmodan inte skulle ligga på en perfekt rak linje, vet du direkt att du har gjort ett räknefel någonstans.

Så knäcker du de vanligaste provuppgifterna

När klockan tickar på högskoleprovet eller ett matteprov handlar det om mer än att bara kunna formlerna utantill. Du måste snabbt kunna se vilken typ av uppgift du har framför dig, välja rätt taktik och styra undan från de vanligaste misstagen. Här blir en riktigt solid förståelse för räta linjens ekvation ditt absolut bästa verktyg.

De flesta uppgifter du stöter på är egentligen bara variationer på några få grundidéer. Lär du dig känna igen dem kommer du kunna lösa frågorna både snabbare och med större säkerhet. Oftast handlar det om att hitta punkten där två linjer korsar varandra, jobba med parallella och vinkelräta linjer eller att kunna tolka information direkt ur en graf.

Låt oss nu dyka ner i de absolut vanligaste frågetyperna. Vi tar ett typiskt exempel för varje och går igenom lösningen, steg för steg.

Hitta skärningspunkten mellan två linjer

En riktig klassiker är att bestämma exakt var två linjer möts. Föreställ dig två vägar som korsar varandra – skärningspunkten är precis den plats där de delar samma koordinater. Matematiken bakom detta är faktiskt förvånansvärt rättfram.

I punkten där linjerna skär varandra är både x- och y-värdena identiska för båda linjerna. Det betyder att vi helt enkelt kan sätta de två ekvationerna lika med varandra för att hitta den gemensamma punkten.

Exempel: Var skär linjerna y = 3x - 1 och y = x + 5 varandra?

1. Sätt ekvationerna lika: Eftersom y är samma för båda i skärningspunkten, måste högerleden också vara lika.
   3x - 1 = x + 5
2. Lös ut x: Nu samlar vi alla x på ena sidan och alla siffror på den andra för att se vad x blir.
   3x - x = 5 + 1
   2x = 6
   x = 3
3. Lös ut y: Nu när vi vet att x-värdet är 3 kan vi stoppa in det i vilken som helst av de två ursprungliga ekvationerna för att få fram y. Vi kan ta den enklare, y = x + 5.
   y = 3 + 5
   y = 8

Svaret är alltså att linjerna korsar varandra i punkten (3, 8). Den här metoden är en grundbult i provmatematiken. Att bemästra den sparar massor av tid och säkrar viktiga poäng. För fler smarta strategier, kolla in våra lösningsguider för den kvantitativa delen.

Ekvationer för parallella och vinkelräta linjer

Det här är en annan personlig favorit hos provkonstruktörerna. Frågor av den här typen testar om du verkligen har koll på vad k-värdet betyder för en linjes lutning och hur den förhåller sig till andra linjer i ett koordinatsystem.

• Parallella linjer: Två linjer är parallella om de lutar exakt lika mycket. Det betyder att de har precis samma k-värde och därför aldrig kommer att korsa varandra.
• Vinkelräta linjer: Två linjer är vinkelräta om de korsar varandra i en perfekt 90-gradig vinkel. Det sker om produkten av deras k-värden är -1. Alltså: k₁ * k₂ = -1.

Exempel: Bestäm ekvationen för en linje som är parallell med y = 2x + 7 och som går genom punkten (3, 10).

1. Hitta rätt k-värde: Den nya linjen ska vara parallell med y = 2x + 7. Det betyder att den måste ha exakt samma lutning, alltså k = 2.
2. Använd enpunktsformeln (eller y = kx + m): Vi vet nu att vår nya linje har formen y = 2x + m. Nu återstår bara att hitta m.
3. Hitta m-värdet: Vi vet att linjen passerar genom (3, 10). Då sätter vi in x=3 och y=10 i ekvationen för att lösa ut m.
   10 = 2(3) + m
   10 = 6 + m
   m = 4

Den sökta ekvationen är alltså y = 2x + 4.

Tanken att använda ekvationer för att beskriva samband i världen är långt ifrån ny. Räta linjens ekvation har varit ett centralt verktyg ända sedan antikens Grekland. I svenska skolor började den användas mer systematiskt under första halvan av 1900-talet. Redan 1920 finns det dokumenterat i Stockholm hur ekvationen användes för att illustrera samband mellan exempelvis hastighet och tid i fysikundervisningen, vilket var en hörnsten i den tidiga tekniska utbildningen.

Vanliga frågor och snabba svar

Även efter att ha räknat sig igenom exempel och läst om formler kan det finnas små frågetecken som hänger kvar. Det är helt normalt. Tänk på den här delen som en lathund – här får du raka, snabba svar på de vanligaste funderingarna kring räta linjens ekvation.

Inga långa utläggningar, bara klara besked. Vi benar ut allt från specialfall som helt platta linjer till den där lite kluriga skillnaden mellan en ekvation och en funktion.

Vad händer om k-värdet är noll?

En klockren fråga! När k = 0 betyder det helt enkelt att linjen inte lutar alls. Den går varken uppför eller nedför. Tänk dig en helt platt väg.

Ekvationen blir då y = 0 · x + m, vilket ju bara blir y = m.

Det här säger oss att oavsett vilket x-värde vi väljer, så kommer y-värdet alltid att vara m. Resultatet i ett koordinatsystem? En perfekt horisontell linje som skär y-axeln på höjden m.

Hur ser jag snabbt om en punkt ligger på linjen?

Det finns ett superenkelt knep för det här, ett slags "sanningstest". För att kolla om en punkt, säg (a, b), verkligen ligger på linjen sätter du helt enkelt in punktens koordinater i linjens ekvation.

Stämmer ekvationen när du sätter in x = a och y = b? Perfekt, då ligger punkten på linjen. Om det blir en matematisk osanning, som att 5 = 6, då ligger punkten utanför.

Exempel: Ligger punkten (2, 7) på linjen y = 3x + 1?

Vi testar! Sätt in x = 2 och y = 7:
7 = 3(2) + 1
7 = 6 + 1
7 = 7

Jajamän, det stämmer! Alltså ligger punkten (2, 7) på linjen.

Finns det vertikala linjer och hur ser deras ekvation ut?

Absolut! En vertikal linje går rakt upp och ner, som en flaggstång. Den är parallell med y-axeln. Problemet är att dess lutning är "oändlig", så den vanliga formen y = kx + m fungerar inte här.

Istället har en vertikal linje en betydligt enklare ekvation: x = c.

Det betyder att x-värdet är låst och alltid är samma (c), oavsett vad y-värdet är. Ekvationen x = 4 beskriver till exempel en linje där alla punkter har x-koordinaten 4. Några exempel är (4, 0), (4, 5) och (4, -10).

Vad är skillnaden mellan en linjär funktion och en ekvation?

Den här är lite hårfin men viktig för förståelsen. De ser nästan likadana ut, men idén bakom dem skiljer sig åt en aning.

• En räta linjens ekvation (som y = 2x + 3) är ett villkor. Den säger att alla punkter (x, y) som uppfyller just det här sambandet ligger på en och samma linje. Det är ett geometriskt påstående.
• En linjär funktion (som f(x) = 2x + 3) är mer som en maskin. Du stoppar in ett värde (x) och funktionen spottar ut ett nytt värde (f(x), som är samma sak som y). Fokus ligger på relationen mellan input och output.

I praktiken använder vi dem ofta på samma sätt när vi ritar grafer, men det kan vara bra att känna till den lilla skillnaden i perspektiv.