Hur räknar man procent? En praktisk guide för vardagen

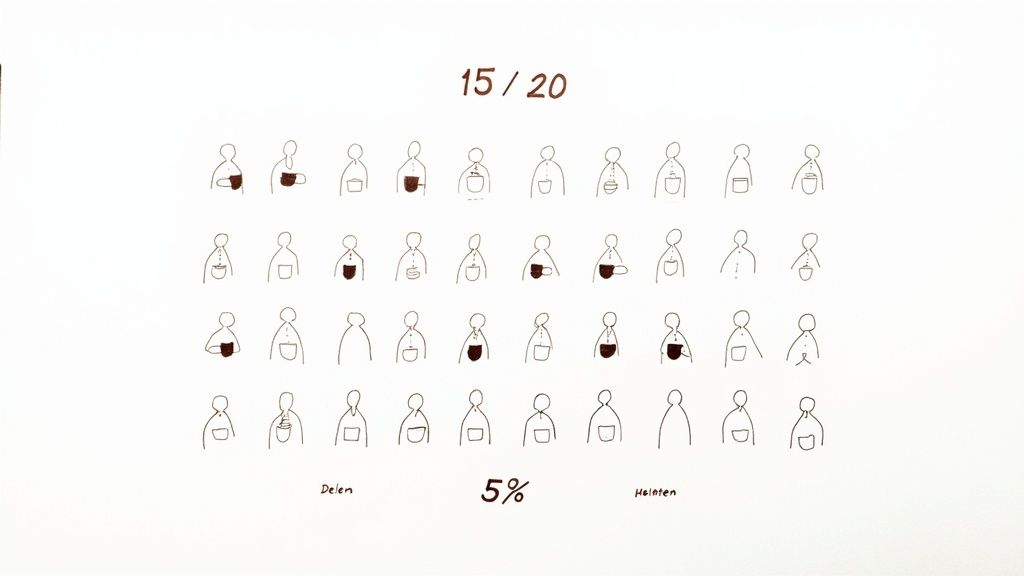
Att räkna ut procent är egentligen ganska rakt på sak. Kärnan i det hela är en enkel formel: (Delen / Helheten) × 100 = Procenten. Tänk dig att 15 av 20 personer i ett rum dricker kaffe. Då blir uträkningen (15 / 20) × 100, vilket är 75 %.

Den här grundprincipen är nyckeln till nästan all procenträkning du kommer stöta på, oavsett om det är på jobbet, i butiken eller när du läser nyheterna.

Hur procenträkning fungerar i praktiken

Att förstå procent är en superkraft i vardagen. Det hjälper dig att snabbt avgöra om en rea verkligen är så bra som den låter eller att förstå ekonomiska nyheter. Många tycker det känns krångligt, men logiken är oftast enklare än man tror.

Allt handlar om att kunna skilja på tre begrepp:

• Delen: Det är den specifika siffra du tittar på. I vårt kaffeexempel är det de 15 personerna som dricker kaffe.
• Helheten: Detta är den totala summan eller det ursprungliga värdet. I samma exempel är helheten hela gruppen på 20 personer.
• Procenten: Det är resultatet – delen uttryckt som en andel av helheten. Alltid i hundradelar.

Kan du identifiera dessa tre i ett problem? Då är du redan mer än halvvägs till lösningen.

De tre vanligaste procentproblemen

I princip alla procentuppgifter du möter kan kokas ner till tre grundläggande varianter. Att snabbt känna igen vilken typ av problem du står inför är det viktigaste steget för att lösa det snabbt och rätt.

Dessa tre scenarier täcker allt från att räkna ut moms och rabatter till att förstå statistik i en rapport eller tolka en löneökning.

Tänk på procent som ett sätt att jämföra saker. Det sätter siffror i ett sammanhang som gör dem lättare att greppa. En prissänkning på 200 kr säger inte lika mycket som 25 % rabatt – procenten avslöjar ju hur stor sänkningen är i förhållande till originalpriset.

För att ge dig en snabb överblick har vi sammanställt de tre vanligaste beräkningarna i en tabell. Se den som en fusklapp du kan kika på när du känner dig osäker på vilken formel som gäller.

Översikt av vanliga procentberäkningar

Här är en sammanfattning av de tre grundläggande sätten att räkna med procent och deras formler.

Typ av beräkning	Fråga som besvaras	Grundformel
Hitta delen	Vad är X % av Y?	(Procent / 100) × Helheten = Delen
Hitta procenten	Hur många procent är X av Y?	(Delen / Helheten) × 100 = Procent
Hitta helheten	Om X är Y %, vad är då 100 %?	Delen / (Procent / 100) = Helheten

När du väl har fått grepp om de här tre metoderna kommer du märka att det mesta faller på plats. Målet med den här guiden är att ge dig verktygen – och självförtroendet – att hantera procent i alla lägen.

Beräkna rabatten eller momsen på ett pris

Att snabbt kunna räkna ut vad en viss procent egentligen betyder i kronor och ören är nog en av de mest användbara mattekunskaperna i vardagen. Det är precis den här typen av procenträkning som hjälper dig att se vad rean faktiskt sparar dig, förstå hur mycket moms du betalar eller räkna ut vad löneökningen egentligen ger i plånboken.

Grundtanken är ganska enkel: omvandla procentsatsen till decimalform och multiplicera den sedan med det totala beloppet. Formeln kan skrivas som (Procent / 100) × Helheten = Delen.

Det låter kanske lite krångligt, men häng med så ser du att det är busenkelt i praktiken. Säg att du hittar en jacka för 800 kr med 25 % rabatt. Då gör du så här:

1. Börja med att göra om procenten till ett decimaltal: 25 / 100 = 0,25
2. Ta sedan decimaltalet och multiplicera det med priset: 0,25 × 800 kr = 200 kr

Rabatten blir alltså 200 kr, vilket betyder att du betalar 600 kr för jackan. Samma logik funkar i alla liknande situationer.

Exempel från verkligheten

Låt oss ta ett annat vanligt scenario – moms. När du handlar i en svensk butik är momsen nästan alltid inbakad i priset du ser. Men ibland, speciellt om du är företagare, visas priser utan moms.

Sverige har ju olika momssatser: 25 % är standard, 12 % gäller för livsmedel och 6 % för saker som böcker och resor. Om en pryl kostar 800 kronor exklusive moms, blir själva momsbeloppet (25 / 100) × 800 = 200 kronor. Vill du dyka djupare i olika procentberäkningar kan du läsa mer på studybuddy.se.

Metoden är lika användbar för dina inkomster som för dina utgifter. Föreställ dig att du får en löneförhöjning på 3 % och din nuvarande månadslön är 30 000 kr. Vad blir det i rena pengar?

• Gör om procenten: 3 / 100 = 0,03
• Multiplicera med lönen: 0,03 × 30 000 kr = 900 kr

Helt plötsligt har du 900 kr extra varje månad. Inte illa!

Tricket är att bli snabb på att omvandla procent till decimalform i huvudet. Tänk att procenttecknet (%) bokstavligen betyder "per hundra". Då blir 15 % samma sak som 15/100, alltså 0,15. När det sitter blir huvudräkningen plötsligt mycket enklare.

När du väl bemästrar det här kan du fatta smartare ekonomiska beslut, oavsett om du är på jakt efter bästa reapriset, kollar lönespecen eller sätter upp en budget. Det handlar helt enkelt om att kunna översätta en abstrakt procentsats till ett konkret värde du faktiskt kan förhålla dig till.

Räkna ut andelen i procent

Hur stor del av lönen slukar hyran varje månad? Eller hur många procent av kollegorna svarade faktiskt på den där enkäten? Att kunna räkna ut andelen är en av de mest användbara mattefärdigheterna i vardagen. Det handlar om att sätta siffror i ett sammanhang.

Principen är enkel: du jämför en specifik del med den stora helheten. Formeln du behöver är lika simpel som den är kraftfull: (Delen / Helheten) × 100.

Det som kan vara lite klurigt är att snabbt identifiera vad som är "delen" och vad som är "helheten" i en uppgift, särskilt när den är formulerad som en längre text.

Se till att du identifierar delen och helheten rätt

För att formeln ska fungera måste du vara säker på vilken siffra som är vilken. Helheten är alltid det totala antalet, det ursprungliga värdet eller den grupp som allt jämförs mot. Delen är den mindre mängd du vill veta andelen av.

Vi tar ett konkret exempel. I en klass går det 25 elever. Av dessa är det 15 som cyklar till skolan varje dag.

• Helheten: Det totala antalet elever, alltså 25.
• Delen: De som cyklar, det vill säga 15.

Nu sätter vi in siffrorna i formeln: (15 / 25) × 100.

Här ser vi direkt att det blir ett bråktal, 15/25. Om du känner dig osäker på hur man hanterar division och bråk kan det vara en bra idé att fräscha upp minnet. Vår guide om att räkna med bråktal kan ge dig precis den repetition du behöver.

Procent är i grunden ett sätt att göra siffror jämförbara. Att 15 av 25 elever cyklar är samma andel som 30 av 50. Båda blir 60 %, en siffra som är lätt att förstå och relatera till oavsett de ursprungliga talen.

Uträkningen blir 0,6, som vi sedan multiplicerar med 100 för att få procent. Svaret är alltså att 60 % av eleverna cyklar till skolan.

Så används det i verkligheten

Den här typen av uträkning ser du överallt, inte minst i officiell statistik som formar vår bild av samhället. Statistiska centralbyrån (SCB) använder exakt den här metoden för att beskriva allt från arbetslöshet till utbildningsnivå.

Till exempel visade deras siffror för 2023 att ungefär 47,5 % av svenskarna mellan 25 och 64 år hade en eftergymnasial utbildning. Här har man tagit antalet personer med högskoleutbildning (delen) och delat det med det totala antalet personer i åldersgruppen (helheten).

Det här visar verkligen hur en enkel formel kan omvandla stora datamängder till en enda, begriplig siffra. När du väl behärskar detta blir du inte bara bättre på matte – du blir också bättre på att förstå och kritiskt granska informationen du möter varje dag.

Att förstå procentuell ökning och minskning

Världen är i ständig rörelse. Priser på mat går upp, värdet på aktier svänger och befolkningen i en stad förändras. För att verkligen kunna greppa och sätta siffror på dessa förändringar är det helt avgörande att veta hur man räknar ut procentuell ökning eller minskning. Det är nyckeln till att analysera trender och fatta smarta beslut, oavsett om det gäller din privatekonomi eller hur du tolkar nyheterna.

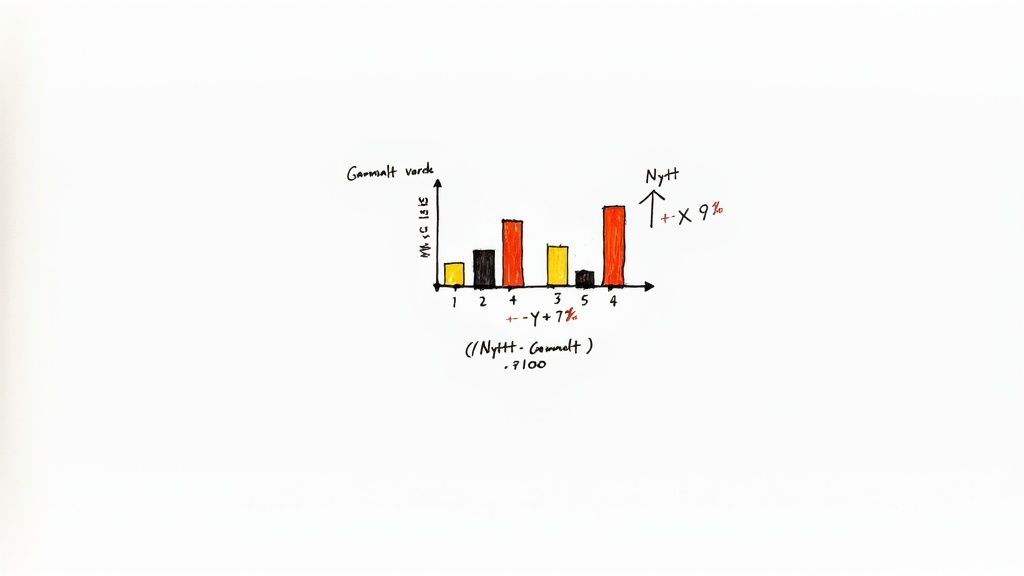
Kärnan i det hela är en enkel men kraftfull formel: ((Nytt värde - Gammalt värde) / Gammalt värde) × 100.

Formeln sätter förändringen i relation till det ursprungliga värdet, vilket ger en rättvis bild av hur stor den faktiskt är. Får du ett positivt svar är det en ökning. Blir det negativt, ja, då är det en minskning.

Så räknar du ut procentuell förändring

Låt oss göra det konkret. Tänk dig att din månadshyra höjs från 9 000 kr till 9 450 kr. Hur stor är ökningen i procent?

Först identifierar vi våra värden:

• Gammalt värde: 9 000 kr
• Nytt värde: 9 450 kr

Sedan sätter vi in siffrorna i formeln: ((9 450 - 9 000) / 9 000) × 100.

Uträkningen blir då: (450 / 9 000) × 100 = 0,05 × 100 = 5 %.

Hyran har alltså ökat med 5 %. Exakt samma princip gäller för minskningar. Om en tröja som från början kostade 500 kr reas ut för 400 kr blir uträkningen ((400 - 500) / 500) × 100, vilket landar på -20 %.

Den här typen av beräkning är central för att förstå ekonomiska begrepp som inflation. I Sverige används den flitigt för att följa prisutvecklingen. Enligt SCB:s prognos för konsumentprisindex (KPI) för 2024 låg inflationen på 2,0 %, vilket helt enkelt betyder att den allmänna prisnivån förväntades stiga med just den procentsatsen. Vill du gräva djupare kan du lära dig mer om hur procenträkning används i ekonomin.

Procent eller procentenheter – en vanlig fälla

Här kommer en viktig detalj. När man pratar om förändringar i procenttal är det extremt lätt att trampa fel och blanda ihop begreppen procent och procentenheter. Det här är ett av de allra vanligaste misstagen, särskilt när man tolkar statistik om räntor, valresultat eller arbetslöshet.

Procentenheter beskriver den absoluta skillnaden mellan två procenttal. Procent beskriver den relativa förändringen.

Tänk dig att bolåneräntan stiger från 2 % till 3 %. Vad har hänt?

• I procentenheter: Skillnaden är 1 procentenhet (3 - 2 = 1). Enkelt och rakt på sak.
• I procent: Ökningen är hela 50 % ((3 - 2) / 2) × 100.

Båda sätten att beskriva förändringen är korrekta, men de berättar helt olika historier. Att förstå skillnaden är avgörande för att kunna se igenom missvisande rubriker och korrekt bedöma hur stor en förändring egentligen är. När du väl har koll på det här kan du analysera data på en helt ny nivå. Det är en ovärderlig färdighet.

Smarta knep för snabb huvudräkning

Att kunna slänga ihop en procentuträkning i huvudet är en riktig superkraft i vardagen. Med några enkla knep blir du snabbare än miniräknaren, oavsett om du står i en butik och klurar på en rabatt eller vill räkna ut dricksen på restaurangen.

Det absolut bästa tricket, och det du kommer ha mest nytta av, är att snabbt kunna hitta 10 % av ett tal. Det gör du busenkelt genom att flytta kommatecknet ett steg åt vänster. Om en vara kostar 450 kr, så är 10 % alltså 45 kr.

När du väl har koll på 10-procentaren öppnas en helt ny värld av snabba uträkningar.

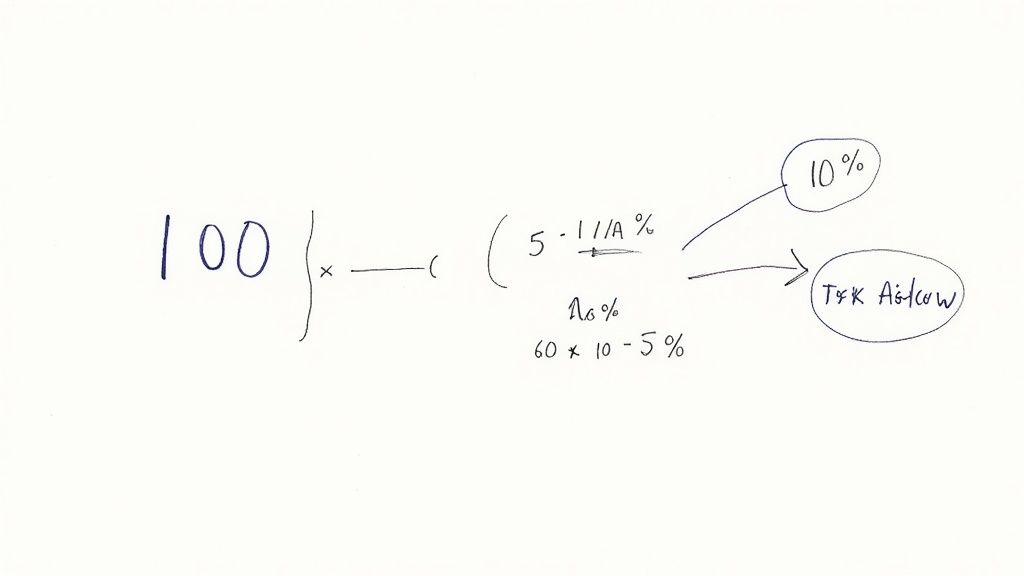
Bygg vidare från 10 procent

Genom att utgå från 10 % kan du lätt som en plätt hitta andra vanliga procentsatser. Det är en strategi som fungerar förvånansvärt ofta och som snabbt ger dig en bra magkänsla för vad saker och ting landar på.

Här är några exempel på hur du kan tänka:

• Hitta 5 %: Det är ju helt enkelt hälften av 10 %. Om 10 % av 450 kr är 45 kr, så blir 5 % hälften av det, alltså 22,50 kr.
• Hitta 20 %: Detta är dubbelt så mycket som 10 %. I vårt exempel blir det alltså 2 × 45 kr = 90 kr.
• Hitta 1 %: Flytta kommatecknet ett steg till. 1 % av 450 kr blir 4,50 kr. Och när du vet vad 1 % är kan du enkelt räkna ut 2 % (9 kr) eller 7 % (7 × 4,50 kr = 31,50 kr).

Den här metoden handlar egentligen om att bryta ner ett lite knepigare problem i mindre, mer hanterbara delar. Det är en grundläggande teknik som är otroligt användbar i många matematiska sammanhang. Faktum är att många av principerna ingår i kursen Matematik 1, och vill du fräscha upp minnet kan du kika på vårt formelblad för Matte 1b.

Kombinera olika procenttal

Nu till det riktigt finurliga: att kombinera de enkla procenttalen för att knäcka mer komplexa uträkningar. Säg att du vill räkna ut en rabatt på 35 % på en tröja som kostar 600 kr. Istället för att gräva fram mobilen kan du tänka så här:

1. Börja med 10 %: 10 % av 600 kr är 60 kr.
2. Räkna ut 30 %: Det är tre gånger 10 %, alltså 3 × 60 kr = 180 kr.
3. Hitta 5 %: Det är hälften av 10 %, så 60 kr / 2 = 30 kr.
4. Lägg ihop dem: 30 % + 5 % = 180 kr + 30 kr = 210 kr.

Rabatten är alltså 210 kr. Lätt! Ett annat sätt att räkna ut 45 % är att först ta 50 % (hälften) och sedan dra ifrån 5 %. På 600 kr blir det 300 kr - 30 kr = 270 kr.

Genom att träna på dessa metoder bygger du upp en mental snabbhet. Det handlar inte om att vara ett mattegeni, utan om att ha en verktygslåda med smarta genvägar som fungerar i verkliga situationer.

Öva på typiska uppgifter från Högskoleprovet

Att kunna räkna med procent är mer än bara en bra vardagskunskap – det är en av de absolut viktigaste pusselbitarna för att knäcka den kvantitativa delen på Högskoleprovet. Provet är fullt av uppgifter som är skapade just för att testa om du kan identifiera rätt metod och räkna snabbt under press.

Vid första anblicken kan många av uppgifterna se krångliga ut. Men skrapar man lite på ytan inser man snabbt att de nästan alltid bygger på någon av de grundläggande procentberäkningarna vi gått igenom.

Nyckeln är att träna upp sitt "procent-öga". Genom att nöta uppgifter som liknar de som faktiskt kommer på provet lär du dig att direkt se vilken formel eller metod som passar bäst. Ett hett tips är att plöja igenom gamla HP-prov, det ger en oslagbar känsla för hur frågorna är formulerade och vilken svårighetsgrad du kan förvänta dig.

Ett klassiskt exempel – och en vanlig fälla

Låt oss kika på en uppgift som dyker upp i olika former gång på gång. Tänk dig att priset på en vara först höjs med 20 % och därefter sänks med 20 %. Vad blir den totala prisförändringen i procent?

Här är det lätt att gå i fällan. Den första tanken för många är att svaret måste vara noll, eftersom höjningen och sänkningen är lika stora. Men det är fel. Anledningen är att den andra procentuella förändringen beräknas på ett nytt värde.

Så här bryter vi ner det:

1. Välj ett enkelt startvärde. Låt oss säga att varan kostade 100 kr från början. Det gör alla beräkningar mycket enklare.
2. Räkna ut prishöjningen. En ökning med 20 % på 100 kr är 20 kr. Det nya priset landar alltså på 120 kr.
3. Räkna ut prissänkningen. Nu kommer det viktiga: sänkningen på 20 % ska beräknas på det nya priset, 120 kr. Sänkningen blir alltså 0,20 × 120 = 24 kr.
4. Vad blir slutpriset? Vi drar bort sänkningen från det höjda priset: 120 kr - 24 kr = 96 kr.

Vi startade på 100 kr och slutade på 96 kr. Den totala förändringen är en minskning med 4 kr, vilket motsvarar en total prissänkning på 4 %.

Proffstips: Ställs du inför en uppgift med procent på procent på Högskoleprovet? Välj alltid 100 som utgångsvärde. Det förenklar huvudräkningen dramatiskt och minskar risken för slarvfel när klockan tickar.

Genom att aktivt leta efter den här typen av vanliga tankevurpor och öva på liknande problem bygger du upp den snabbhet och den säkerhet som krävs för att plocka värdefulla poäng på provdagen.

Vanliga frågor och funderingar kring procent

Här tar vi en titt på några av de vanligaste frågorna som dyker upp när man börjar räkna med procent. Tanken är att snabbt reda ut eventuella frågetecken och hjälpa dig att undvika typiska fällor, så att du kan känna dig säker på dina uträkningar.

Vad är skillnaden mellan procent och procentenheter?

Det här är nog den absolut vanligaste källan till förvirring, och det är lätt att förstå varför. Men egentligen är det ganska logiskt när man väl knäcker koden.

Procentenheter beskriver den raka, absoluta skillnaden mellan två procenttal. Procent, å andra sidan, handlar om den relativa förändringen.

Tänk dig en bolåneränta som går upp från 2 % till 4 %. Då kan man säga att den har ökat på två olika sätt:

• Med 2 procentenheter (det är den enkla skillnaden: 4 - 2 = 2)
• Med 100 procent (den har ju fördubblats, vilket är en relativ ökning: ((4 - 2) / 2) × 100 = 100 %)

Att ha koll på den här skillnaden är A och O för att kunna tolka nyheter, statistik och ekonomiska rapporter på rätt sätt.

Hur räknar man procent baklänges?

Ibland vet du vad något är efter en procentuell förändring och vill ta reda på vad det var innan. Det här kallas ofta för att räkna baklänges och är superanvändbart för att se vad en vara kostade innan en rea eller en prishöjning.

För att hitta det ursprungliga värdet använder du formeln: Ursprungligt värde = Slutvärde / Förändringsfaktor.

Låt oss ta ett exempel. En jacka kostar nu 960 kr efter att priset höjts med 20 %. För att hitta originalpriset delar du helt enkelt det nya priset med förändringsfaktorn, som i det här fallet är 1,20.

Uträkningen blir då 960 / 1,20 = 800 kr. Jackans ursprungliga pris var alltså 800 kr.